The Fourth Dimension

Updated 7/16/19: Added gifs

For probably about a decade now, I have had an interest in attempting to imagine in my head things that can’t be seen with our eyes, like colors not on the visible spectrum, and a fourth spatial (i.e. not time) dimension. While I’ve all but given up on imagining a new color, I’ve made some progress on the fourth dimension as it is highly mathematical and can thus be reasoned through to a certain degree. I recently had an attempt that was relatively effective, and figured I’d share.

The foundation that much of my thought process is built on is that we can think about lower-dimension universes and scale the concepts up to our 3D universe. When looking at a 2D universe, we have the higher-dimension viewpoint, but can easily imagine the difficulties they would have imagining a 3D universe. This is very similar to the struggle of someone in a 3D universe imagining a 4D universe.

I like to use objects rotating as my main point of imagination. It is a good way to picture how things behave in a given number of dimensions, and it’s also just fascinating to me that in a 4D universe, things rotate about a plane rather than a line, which I will explain shortly.

If you imagine a 2D world, it is basically a comic strip, with no depth involved; the inhabitants can only view along the plane of the paper, not into or out of it. If the inhabitants only have one eye, they will only see one dimension – a line of vision that can be various colors. This is equivalent to us, in our 3D inhabitance, only seeing 2 dimensions with either given eye. With two eyes, we can pick up depth perception of the things we can see, but we still really only have a plane (2 dimensions) of vision, because we can’t see multiple objects along a single line originating from our eye; the first one will block us from seeing anything beyond it. Similarly, a 2D observer with two eyes would have depth perception, but also could still only fully see in one fewer dimension than it occupies – meaning a line of vision.

Here’s a bird’s eye view of a 2D person looking at a box, and what that person actually sees.

Note that no 2D person would ever be able to see the left frame above, because it requires you to exit the plane they exist in and look at it from there, but doing so requires a third dimension to exist. As an interesting aside, if a 2D person were to walk around another 2D person, observing them, they could only ever see the outer edge of the other person. Similarly, we can only ever see the outer surface of another person in 3D, but we can see the inside of a 2D person, not just its edge. Scaling this up, a 4D observer would be able to see the entire inside of a 3D person, not just the outer surface.

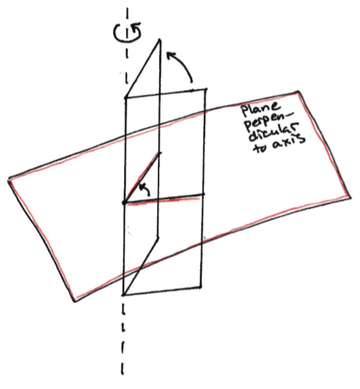
Getting back on topic, a 2D observer could observe a line (or shape, but I’m going to use line because it’s simpler as we scale up) rotating about a point. In 2D, things can only rotate about a point, which is different from 3D, where things rotate about lines. This is because, if you were to try to rotate a line in 2D about another line, the rotation line would need to be in the same plane as the line being rotated, by definition of 2D, and doing so would rotate the line out of the plane, which again is impossible in 2D. So in 2D, things rotate about a point, which is zero dimensional, and in 3D, they rotate about a line, which is one dimensional. Putting this generally, objects will rotate about the infinite shape that is two dimensions lower than the universe the rotation is occurring in. When I say “infinite shape”, I mean the shape that extends infinitely in all directions it exists in – a point is the only possible 0D shape, then in 1D a line extends infinitely and is thus the infinite 1D shape, in 2D it is a plane, and in 3D it is 3-space. If we apply the general rotation scheme to a 4D object, we get that it will rotate about a plane.

It is obviously difficult to, from a 3D point of view, imagine something rotating about a plane, but to aid in doing so, we once again want to look back at 2D and apply what we learn to our perspective. In the same way we struggle to imagine a 3D object rotating about a plane, a 2D observer would struggle to imagine a 2D object rotating about a line, because that can’t happen in their universe, as we already established. If we take said 2D object in question to be a plane, and the axis of rotation to be on that plane, we could recognize this rotation as a series of many lines rotating about points (the 2D rotation we discussed), such that all the points of rotation fall on the same line. Here’s a single slice through the 3D rotation, showing the intersection it makes with the slicing plane.

If a 3D person tried to explain a plane rotating about a line to a 2D person (maybe some other time we can talk about the physics of sound in 2D…), they would likely relay this message. The issue is, the 2D person would not be able to imagine any of those many "lines rotating about points" to be outside their plane, and would thus imagine the following, which is a plane getting distorted, not rotated:

Note that the above is again a bird’s eye view of the 2D person’s perception, and is not a perspective drawing of what actually happens in 3D rotation. In other words, neither of those red parallelograms are supposed to be coming out of or going into the page. But it is not a coincidence that it looks that way. What the 2D observer imagines is the 2D projection of what happens in 3D. All but one of the points of rotation actually fall on different planes than the one the observer is in, but the drawing above is what the shadow of the real rotation would look like. We are equally likely to imagine the 3D projection of what happens in 4D, unless we learn from the mistakes in the 2D person’s perception.

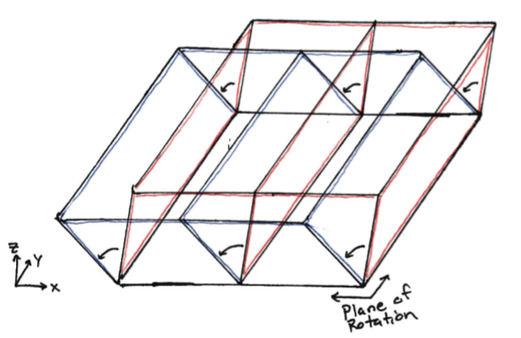
In the way that a plane rotating about a line is a series of lines rotating about points, a 3D object rotating about a plane is a series of planes rotating about lines. These lines of rotation must exist in the same plane, just as the points of rotation must be on the same line in the previous example. When imagining this, we almost inevitably will fall into the same trap as a 2D observer: imagining all of these lines of rotation existing in our 3D world, when in reality only one would. The rest would fall in different 3-spaces along the additional dimension, just as the rest of the points of rotation lied along different planes in the 2D analog. Here’s a representation of what we might imagine when trying to picture rotation about a plane:

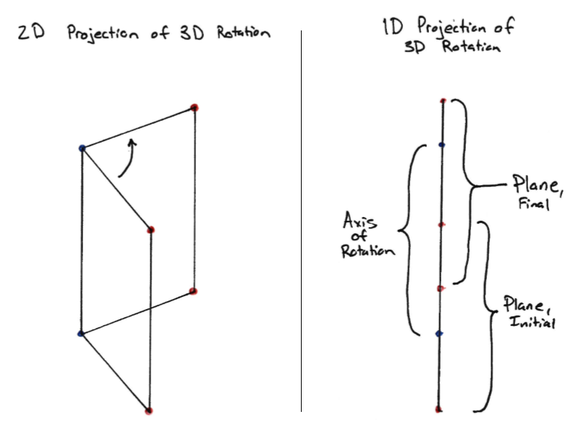
Before I go on, I should point out the absurdity of the above image. I am displaying a 2D representation of the 3D projection of a 4D rotation. Basically, I’m projecting what’s happening down to two whole dimensions fewer than it happened in. This is the same as displaying a 3D rotation in 1D; as in points all falling on a single line. Here’s what that would look like:

Now that we’ve acknowledged the physical limitations of the medium I chose to convey this information, let’s get back on track. A couple paragraphs back I mentioned different 3-spaces. The idea of additional (infinite, in fact) 3-spaces existing at every point along the fourth dimension is not easy to process, and it takes a lot of thought to appreciate the breadth of what that would mean (e.g. my previous point about being able to see the inside of a person in 4D). This is historically where I would get hung up in my attempts to understand 4D, but I recently had an idea that helped break through to a degree.

The natural way of imagining dimensions is to use distances as their measure, but that’s not necessarily the only way to do it. If, instead, we treat one of the dimensions as the “color dimension”, we can think of the other three as what we see around us, and give each 3-space along the color dimension a different color on the visible spectrum. If we overlay all of the differently-colored 3-spaces on our own and observe the colors of the resulting objects, it can tell us where they exist along the color-axis.

To show what this might look like, let’s again look a dimension lower then build from there. I’m going to show how we could display a 3D rotation of a plane about a line on 2 dimensions, using color to demonstrate the dimension we lose in doing so. Here are two examples; in the first, the plane rotates about the color axis, and in the second it rotates about a non-color axis.  Note that all colors overlaid together add up to white, so if the rotating plane exists in the same location at each slice of the color-axis, it will appear white in the color projection. In both images, an isometric view is shown on the left, with the birds-eye view on the right. The image on the right is all a 2D person could see.

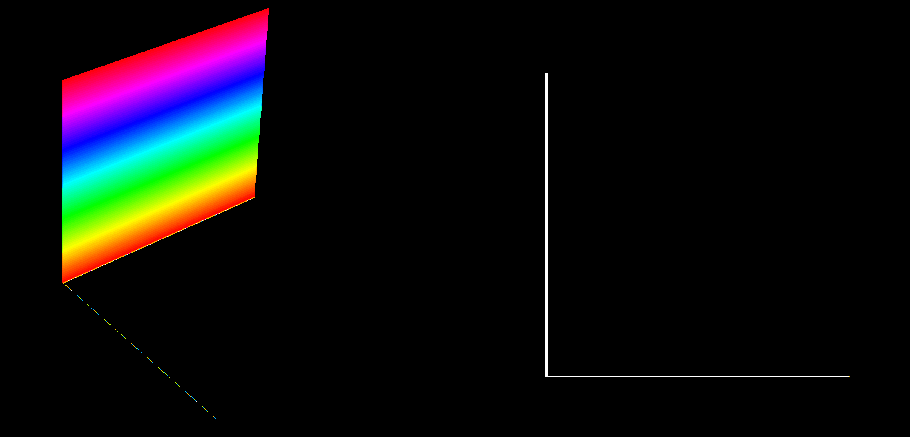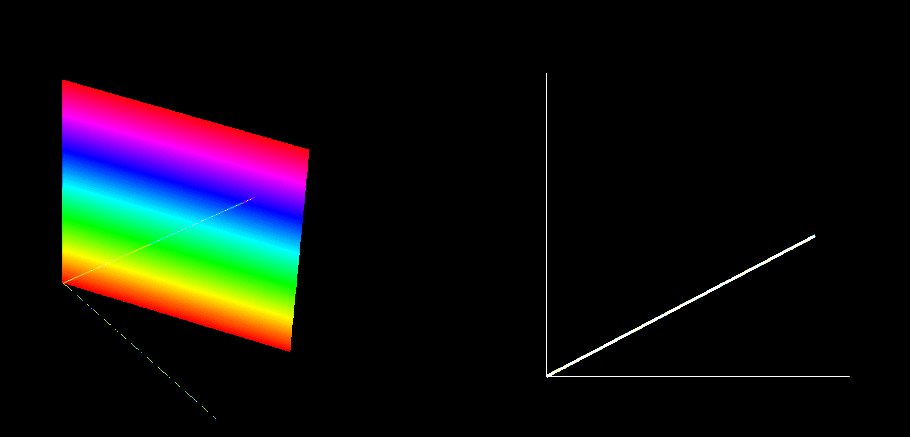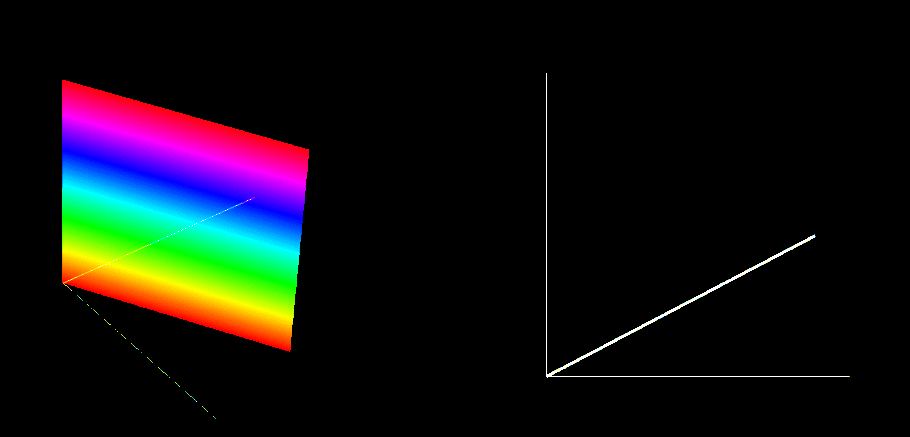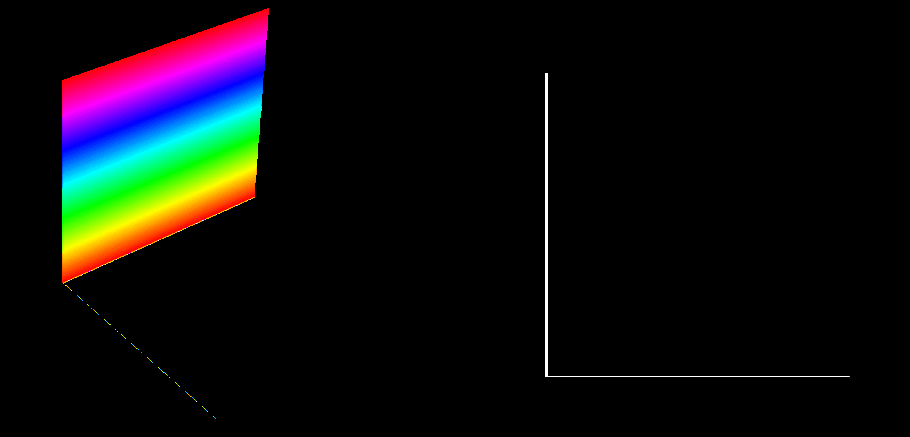
Plane rotating about the color axis

Plane rotating about a non-color axis

An important general rule to recognize here is that, no matter the number of dimensions a rotation happens in, it is a movement between exactly two direction, or axes. In 2D, the point of rotation can be chosen as the origin of the x-y plane, and the rotation itself is between the x and y direction. In 3D, rotation is about a line; by assigning that line to be the z-axis, we once again end up with rotation purely between the x and y direction, while z position is locked for any point being rotated. This scale infinitely, because for each dimension added, the body and the feature that the body rotates about both gain one dimension, and the thus difference remains 2.

If we look at a 4D rotation, the way it looks utilizing the color-axis can be divided into two types: rotations about a plane containing the color-axis, and those about planes not containing the color-axis. If the plane of rotation contains the color-axis, then no motion along the color-axis occurs. This means the entire object will exist in all three (red, blue, green) planes of the color-axis for the entire rotation. This is what happened in the first color-axis-utilizing 3D rotation, above. In an analogous fashion, the 4D rotation about a plane containing the color-axis will just be a white plane (see why I chose a line to rotate in 2D, and not a plane?) that looks like a 3D rotation about a line, that line being the other axis, besides the color-axis, making up the plane of rotation. This is a trivial case, so I won’t bother drawing it. The other case is the interesting one.

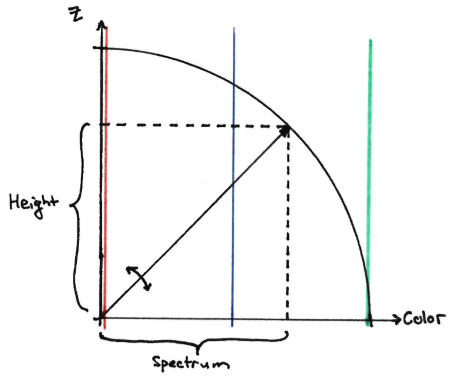
If the color-axis isn’t part of the plane of rotation, then the plane must be defined by two spatial axes. Let’s say the x-y plane is the plane of rotation; this means the cube will be rotating between the z-axis and the color-axis. Let’s look to the trusty ol’ unit circle to see how this works. Note that this also applies to the second color-axis-utilizing 3D rotation, above.

Now, if we put this all together, we can get our depiction of 4D rotation. With the cube starting such that it only exists on one point along the color-axis, we know it will have its full height (z-coordinate), and be entirely red. We’ll treat red to be our 3-space; everything not red is outside of our 3-space. It will then decrease in height and increase along the color-axis, picking up more colors on its spectrum. The x and y coordinates of all the points remain the same by definition, so the box doesn’t shift in either of the sideways spatial dimensions. Eventually, once the box has rotated 90°, it will only occupy one plane along the z-axis, and its third dimension, besides x and y, will be entirely along the color axis, thus it will appear white, and will just be a plane with no height. You can probably notice a parallel between this and the corresponding 3D rotation.

Box rotating about the x-y plane in 4 dimensions

So there you have it – my attempt at visualizing something moving in 4D. I still have more to go before I’d say I really understand it, but I think the color-axis helps. At the very least, I hope some of my readers find it to be an interesting exercise. Now to use temperature as the fifth axis…