As someone who prefers to get around by biking or walking, I tend to notice ways in which car-centric thinking makes things worse. A big one is in the layouts of towns and cities. In the recently-built suburbs of Oregon that I work in now, there are a few main roads that you spend most of your driving time on, and neighborhoods are divided so that they don’t connect main roads, or if they do it’s via a very convoluted path. This prevents rat-running which likely reduces traffic congestion, but it also forces walkers and bikers to take the main roads, which are almost always slower, as they’re not the direct route, and those not in cars are limited by distance, not speed limit. This design was made to accommodate driving, and in turn discourages human-powered transportation, by making it more difficult to do so. Cul-de-sacs have gotten an increasingly bad name over the past few years for the same reason. Even in cities, where disjoint neighborhoods and dead-end roads are much less common, the car-centric design still makes for longer commute distances, which is what I’m going to show here.
Most cities built since the introduction of cars have been laid out in a grid. The grid design certainly predates cars, but before cars, there was at least consideration given to other layouts, whereas with cars as the focus, the grid is chosen without much second thought, since it makes for easier traffic flow planning. If not for this fact, a radial layout would be preferred, as it can be shown that paths are on average shorter in this arrangement. A radial layout is one with a center point, where several roads originate from and go outwards in all directions, with circular (or something close) roads of increasing diameter, all centered at the center point. The roads in the first set are called radial roads, and the second are called tangential roads.
A number of European cities are built partially or fully radially. Moscow is a good example of a radial city, while Paris has sections that are locally radial, connecting to other locally radial sections, but not conforming to an overall radial layout. This is done to allow quick travel between particular landmarks, by making them the center of the local radial layout. This makes sense, as certain spots, like a town center, often draw more people, so there should be roads directly there from all around it – these end up being radial roads. However, even when the destination isn’t at the center of the radial layout, it is still often shorter to get there than on a grid layout.
To test this out, I made a program that picked random locations on a radial city and calculated the distance between them while walking on the radial roads, and the distance between those same points if they were at corners of a grid layout. The outcome depends on how many radial roads there are because more of them means more options, so one of the radial roads is likely to take you to the destination. I made a plot, shown below, of how much shorter, on average, the radial paths between two points were than the grid paths between the same two points. Each data point is the average of 10,000 random pairs on a map with the given number of radial roads.

You can see that more radial roads means more savings. The noise in the data, making it seem like more isn’t always better, is likely due to this being a Monte Carlo style simulation (choosing many random pairs and averaging), but the trend is still fairly clear. It’s worth noting that the grid layout actually has an advantage here, because we’re assuming the two points will fall on street corners, or in other words assuming there are infinitely many grid roads, whereas the radial layout has the possibility of needing to walk a good bit farther to get around blocks. This is shown below, with the grid path in blue and the radial path in purple.

Out of curiosity, and to level the playing field, I ran a simulation with 500 radial roads (effectively infinite), and the percent savings seems to top out at ~14%.
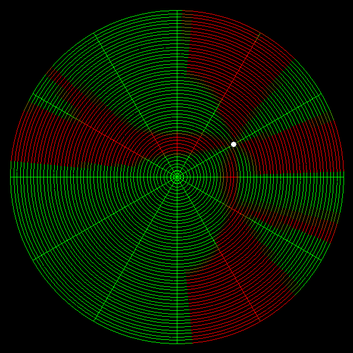
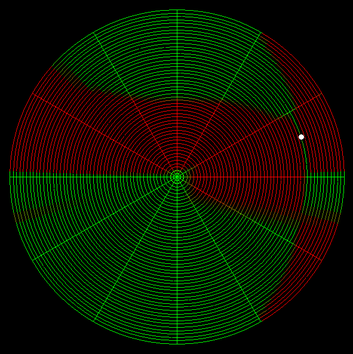
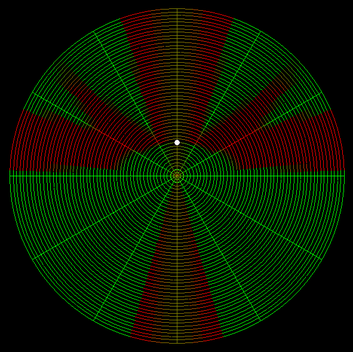
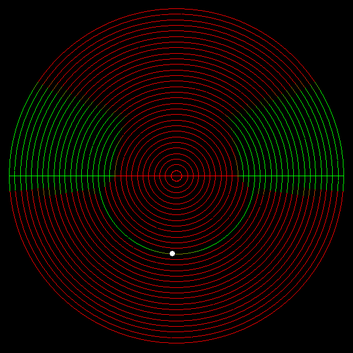
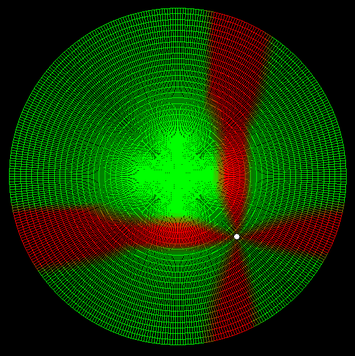
To get a better idea for how the two compared, I decided to make a map of a radial city with a starting point, then color-code the streets to show where it would be faster to walk to on a radial layout and where it would be faster on a grid. The outcome depends on the number of radial roads, as well as the starting point. Here are a few of my favorite ones. Green means radial is faster, red means grid is faster. Number of tangential roads doesn’t change the savings, so I added a lot because that makes the images more clear. Click to enlarge
One last thing that some geometrically-inclined readers may have noticed is that the tangential roads are inefficient because they take a non-straight line path between their two end points. It’s more efficient for them the be straight lines than curves. Doing this would change the tangential roads from circles to n-sided regular polygons, where n is the number of radial roads, with corners at the intersections with the radial roads. When this is done, the upper savings limit is still ~14%, because at larger numbers of radial roads this effect is smaller, but at smaller numbers of radial roads, which is more realistic anyway, it could add 2-3% more savings on top of what’s shown in the plot above.


Write a comment