The Optimal Path on a Grid

One night, a few months ago, I was walking home alone. As my mind wandered, I decided to find the optimal way to walk between two points on a city grid. My hometown was not designed on a grid, so the shortest path between two points was usually clear. On a grid, however, there are many paths that are the same distance:

All four paths shown are 10 block lengths long, and there are a total of 252 paths of that length. If there are so many different paths that are all the shortest distance, how do we find the optimal one among them?

The key is to look at other factors that could impact the time it takes to complete the journey, besides distance. One example is topography – if there was a steep hill in the bottom left of the image above, the orange path wouldn’t be a good choice, since you’d have to walk up then down a hill, slowing you down. However, most cities on a grid are relatively flat, so we’ll ignore that. Another example is walking speed, but that doesn’t really change, except when the slope you’re walking on changes, which we just said we’re ignoring.

The final significant factor in how long a trip takes by foot, especially in cities, is time spent waiting to cross the street. So the key to optimizing a trip on a grid (assuming no areas you specifically want to see/avoid on the way) is to minimize that time spent waiting. To find the best way to do this, I’ll use a new concept called “walking potential”.

Walking potential gets the second half of its name from similar concepts in science, like potential energy. A “potential” is just a measurement of how much, well, potential something has to achieve something else, given its current state. In the case of gravitational potential energy, the potential measures how much energy, in the form of speed, an object could pick up if dropped from its current height. Gravitational potential energy therefore gets larger as the object in question moves farther up. Walking potential, on the other hand, is a measure of how many block lengths you can walk in the direction of your destination without crossing the street. This image shows the walking potential at each corner of each block, given the star is the destination.

Besides rotation, there are only two types of blocks in terms of walking potential. Blocks in the same row/column as the destination have two corners with potential 0, and two with potential 1. All other blocks have one corner with potential 0, two with potential 1, and one with potential 2. This is always true on a perfect grid, and is the key to finding the optimal path.

To reduce the amount of time spent waiting to cross the street, you want to keep your walking potential as high as possible, because the only time you need to wait is when your potential is 0. If your walking potential is greater than 0, that means you have some distance to walk in the direction of your destination without crossing the street, so by definition there’s no need to wait.

So how do you keep your walking potential high? Let’s start with what to do when starting from a walking potential of 2. This part is pretty intuitive, though it may sound foreign, given the new terminology.

Your potential is never going to be higher than 2, meaning the only thing that makes sense to do then is to walk to either of the corners on the same block with potential 1. Once you get to a corner with potential 1, there will likely be a corner across the street that has potential 2. If you can cross the street then, or if you can tell by the traffic signals that you’ll be able to cross soon, then do so, and repeat. Otherwise, continue walking to the corner with potential 0. At that corner, it probably makes sense to cross both streets since by the time you cross in one direction, the other is probably about to get the right-of-way. This will likely land you back on another corner with potential 2, where you repeat the same strategy.

The only places where a potential 1 corner isn’t across the street from a potential 2 corner, and a potential 0 corner isn’t catty-corner to a potential 2 corner are along the row/column the destination is on, and the corners across the street from those. In these locations, the only thing you can do is walk one block, cross the street, walk one block, cross the street, etc., potentially waiting each time you cross the street. This is inefficient compared to having the option to walk a second block if you can’t cross immediately after walking the first block. Therefore, the key is to avoid those locations, shown in red below, as much as possible.

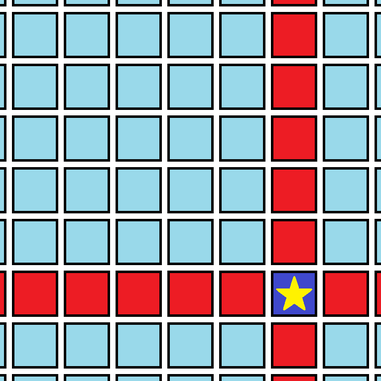
As you can see, the red blocks cut the area into four quadrants, like axes on a graph. Therefore, we’ll call the red row & column the axes of your destination. To avoid the axes, you simply prioritize walking towards the axis that’s farther away. This means when you’re at a corner with potential 2, it’s not an arbitrary decision which potential 1 corner you walk to. You always want to choose the one that’s in the direction of the farther axis. Of course, you’ll end up moving towards the closer axis whenever you walk the second block length because there’s a wait to cross the street at the potential 1 corner. That’s still the right thing to do, but you don’t want to prioritize walking in that direction, or you’ll end up at the axis sooner.

Now, if you make it to a block that’s equally far from either axis, then the direction you prioritize is arbitrary, and you want to zig-zag your way to the destination, never straying more than one block from the blocks that are equal distance from both axes, shown in green below.

The image above features arrows showing the direction you should prioritize walking in when on that block. With this, we can fully define the optimal path to take on a grid:

1. Imagine the red axes originating from your destination, as well as the green axes, which are at a 45° angle to the red axes.

2. When on a corner with potential 2, first walk in the direction of the green axis that’s in the quadrant you’re in. When you get to the potential 1 corner, cross the street if you can, or walk to the potential 0 corner if you can’t, and cross both ways there instead. Do this any time you’re on a blue block.

3. If you reach the green axis, zig-zag your way to your destination, crossing the street whenever you get an opportunity.

4. If you reach a red axis, you’re stuck on it unless you walk away from your destination, which obviously isn’t going to help. Just walk in the direction of your destination.

Following number 2 means walking in the direction that’s closer to the straight line from you to your destination. Interestingly, I previously wrote a post about people naturally doing this, sometimes to their detriment when not on a grid. So maybe humans are coincidentally programmed to take the fastest route on a grid based on instinct.